| 1. Две одинаковые
лодки двигались в озере параллельными курсами со скоростями
V1 и V2 > V1. В тот момент,
когда лодки поравнялись, из первой лодки во вторую переложили
рюкзак. Как при этом изменилась (увеличилась, уменьшилась, не
изменилась) скорость второй лодки? Ответ поясните, указав, какие
физические закономерности вы использовали для объяснения. (Трением
пренебречь).
|
| 2. Пассажир
автобуса на остановке привязал к ручке сиденья за нитку легкий
воздушный шарик, заполненный гелием. Автобус тронулся вдоль
по прямому горизонтальному шоссе, и некоторое время двигался
вперед с постоянным ускорением, затем ехал с постоянной скоростью,
а на подъезде к следующей остановке двигался равнозамедленно,
пока не остановился. Опишите, как менялся угол наклона нити
шарика к вертикали в течение всего времени перемещения автобуса
от одной остановки до другой.
|
| 3. Деревянный
брусок плавает на поверхности воды в миске. Миска покоится на
поверхности Земли. Что произойдет с глубиной погружения бруска
в воду, если миска будет стоять на полу лифта, который движется
с ускорением, направленным вертикально вверх? Ответ поясните,
используя физические закономерности.
|
| 4. В сосуде
плавает кусок льда, а внутри него находится кусок свинца. Что
произойдёт с уровнем воды в сосуде после того, как лед растает?
|
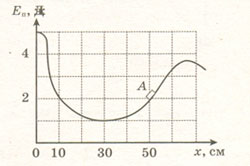
5. После толчка
льдинка закатилась в ямку с гладкими стенками, в которой она
может двигаться практически без трения. На рисунке приведен
график зависимости энергии взаимодействия льдинки с Землей от
её координаты в яме. В некоторый момент времени льдинка находилась
в точке А с координатой х = 50 см и двигалась
влево, имея кинетическую энергию, равную 2 Дж. Сможет ли льдинка
выскользнуть из ямы? Ответ поясните, указав, какие физические
закономерности вы использовали для объяснения. |
|
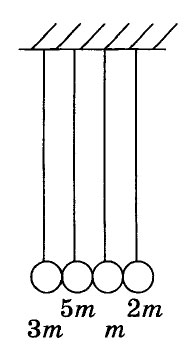
6. Четыре шарика, массы
которых 3m, 5m, m и 2m,
висят, соприкасаясь, на вертикальных нитях. Крайний левый шарик
отклоняют на некоторый угол и отпускают без начальной скорости.
Что произойдет с шариками в результате абсолютно упругого удара? |
|
Приводим авторские решения
некоторых задач: N2, N5,
N6
|